Difficulté : 5/5
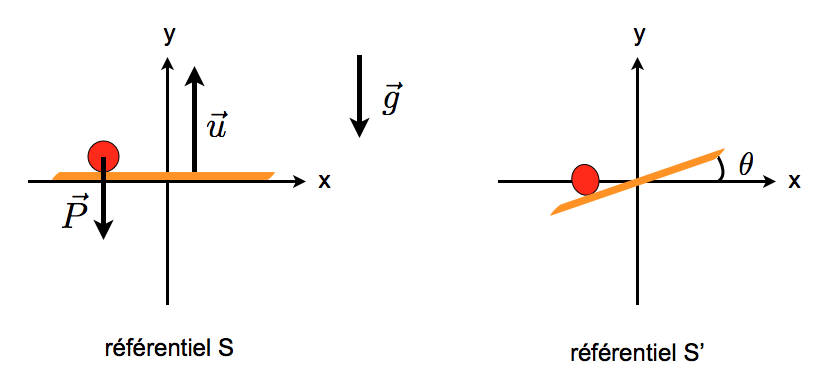
Dans un référentiel S, une plateforme se déplace verticalement à une vitesse \( \vec{u} = u \, \vec{e_y}\).
Considérons le référentiel S' en translation uniforme à la vitesse \( \vec{v} = v \, \vec{e_x}\) par rapport à S. Dans le référentiel S' on démontre sur cette page que la plateforme est inclinée d'un angle \( \theta \) par rapport à l'horizontale, avec \( tan(\theta) = \gamma \frac{v u}{c^2} \) où \( \gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} \).
Considérons un champ gravitationnel \( \vec{g} = -g \, \vec{e_y} \) uniforme dirigé vers le bas.
Dans le référentiel S, la plateforme est horizontale, une bille posée sur la plateforme ne roule pas. Dans le référentiel S' en revanche, la plateforme est inclinée, on pourrait penser que la bille devrait donc se mettre à rouler. La bille ne peut pas à la fois rester immobile dans S et rouler dans S', d'où le paradoxe.
On peut penser au premier examen que les lignes de champ gravitationnel sont, elles aussi, inclinées. Mais cette inclinaison ne pourrait dépendre que de v et en aucun cas de u, or l'inclinaison de la plateforme dépend bien de u.
Cliquez ici pour voir la réponse
Partons de la transformation des forces en RR (les transformations ainsi que la démonstration sont accessibles sur
http://www.sciencebits.com/node/176).
Dans le référentiel S, on a :
- le poids de la bille \( \vec{P} = (0, -p, 0) \)
- sa vitesse \( \vec{u} = (0, u, 0) \)
Dans le référentiel S' en translation à vitesse \((v, 0, 0)\) calculons les
composantes du poids \(\vec{P'}\) :
\( P_x' = \frac{v \, u}{c^2} \, p \)
\( P_y' = -\frac{p}{\gamma} \)
\( P_z' = 0 \)
Calculons maintenant l'angle \( \phi \) que fait le poids avec la verticale, nous avons :
\( tan(\phi) = \left| \frac{P_x'}{P_y'} \right| = \gamma \, \frac{v \, u}{c^2} = tan(\theta) \)
d'où il en résulte que le poids de la bille est perpendiculaire à la plateforme dans le référentiel S'.
Interprétation :
Ce paradoxe illustre ce fait étrange qu'en relativité force et accélération ne sont généralement pas colinéaires, de même le poids n'est pas généralement aligné avec le champ gravitationnel. L'expression du poids d'un objet en chute libre est la suivante :
\( \vec{P} = \frac{d \vec{p} }{dt} = \frac{d(\gamma \, m \, \vec{v} )}{dt} = \gamma \, m\, \vec{g} + \frac{d \gamma}{dt} m \vec{v} \).
